Research
Inverse Problems
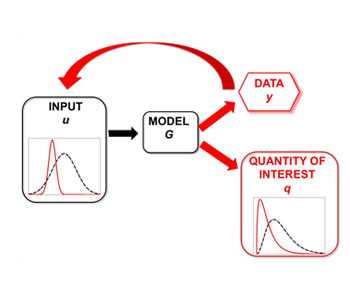 A mathematical model for a physical experiment is a set of equations which relate inputs to outputs. Inputs represent physical variables which can be adjusted before the experiment takes place; outputs represent quantities which can be measured as a result of the experiment. The forward problem refers to using the mathematical model to predict the output of an experiment from a given input. The inverse problem refers to using the mathematical model to make inferences about input(s) to the mathematical model which would result in given measured outputs. The subject of inverse problems in differential equations is of enormous practical importance, and has also generated substantial mathematical and computational innovation. Typically some form of regularization is required to ameliorate ill-posedness. The Bayesian approach to regularization allows for a full characterization of all possible solutions, and their relative probabilities, whilst simultaneously forcing significant modelling issues to be addressed in a clear and precise fashion. Although expensive to implement, this approach is starting to lie within the range of the available computational resources in many application areas. It also allows for the quantification of uncertainty and risk, something which is increasingly demanded in these applications. Furthermore, the approach is conceptually important for the understanding of simpler, computationally expedient approaches to inverse problems. Stuart's work in this area is focussed on the development and exploitation of a rigorous framework for Bayesian inversion on function space, a setting with wide applicability and pratcial relevance. Application to problems in the geophysical sciences provides a driving focus for the work, and development of the methodology in the context of classification of high dimensional data, as arises in the behavioural, information and social sciences, is an on-going theme. Mathematically the primary tools employed are from high dimesional probability, graph theory, partial differential equations and stochastic processes.
A mathematical model for a physical experiment is a set of equations which relate inputs to outputs. Inputs represent physical variables which can be adjusted before the experiment takes place; outputs represent quantities which can be measured as a result of the experiment. The forward problem refers to using the mathematical model to predict the output of an experiment from a given input. The inverse problem refers to using the mathematical model to make inferences about input(s) to the mathematical model which would result in given measured outputs. The subject of inverse problems in differential equations is of enormous practical importance, and has also generated substantial mathematical and computational innovation. Typically some form of regularization is required to ameliorate ill-posedness. The Bayesian approach to regularization allows for a full characterization of all possible solutions, and their relative probabilities, whilst simultaneously forcing significant modelling issues to be addressed in a clear and precise fashion. Although expensive to implement, this approach is starting to lie within the range of the available computational resources in many application areas. It also allows for the quantification of uncertainty and risk, something which is increasingly demanded in these applications. Furthermore, the approach is conceptually important for the understanding of simpler, computationally expedient approaches to inverse problems. Stuart's work in this area is focussed on the development and exploitation of a rigorous framework for Bayesian inversion on function space, a setting with wide applicability and pratcial relevance. Application to problems in the geophysical sciences provides a driving focus for the work, and development of the methodology in the context of classification of high dimensional data, as arises in the behavioural, information and social sciences, is an on-going theme. Mathematically the primary tools employed are from high dimesional probability, graph theory, partial differential equations and stochastic processes.
